I am a researcher in 3D computer graphics and geometry processing.
My interests involve applying numerical optimization techniques to geometric problems with applications in 3D modeling, animation, engineering, biology, and other fields. I have worked on algorithms for high-quality surface mapping and semi-automatic quad mesh generation (re-topology), as well as on tools for automatic differentiation in geometry processing.
I received my B.Sc. and M.Sc. in computer science from RWTH Aachen University and am a PhD candidate at the Visual Computing Institute in Aachen, Germany.
Research
Publication at Eurographics 2023
Surface Maps via Adaptive Triangulations
We compute bijective maps between genus-0 surfaces at adaptive resolutions, independently of the input mesh complexity. The new idea is to represent maps via a common triangulation that only approximates the input surfaces but stays in bijective correspondence to them (via spherical parametrizations). Treating both the connectivity and the geometric embeddings of this triangulation as degrees of freedom allows us to quickly optimize maps in a coarse-to-fine manner. In contrast to previous methods, we manage to avoid the costly computation of overlay meshes and also support mapping between more than two surfaces at once.
This paper received the Günter Enderle Best Paper Award at Eurographics 2023 as well as the Graphics Replicability Stamp.
Patrick Schmidt, Dörte Pieper, Leif Kobbelt. 2023. Computer Graphics Forum.
Publication at Symposium on Geometry Processing 2022
TinyAD: Automatic Differentiation in Geometry Processing Made Simple
At SGP 2022, we published TinyAD: a lightweight C++ library for automatic differentiation in geometry processing. It computes first and second order derivatives of sparse problems on meshes, by differentiating small subproblems efficiently. TinyAD makes it very easy to experiment with non-linear objective functions and algorithms.
This paper received the Best Paper Award (1st Place) at SGP 2022 as well as the Graphics Replicability Stamp.
Patrick Schmidt, Janis Born, David Bommes, Marcel Campen, Leif Kobbelt. 2022. Computer Graphics Forum.
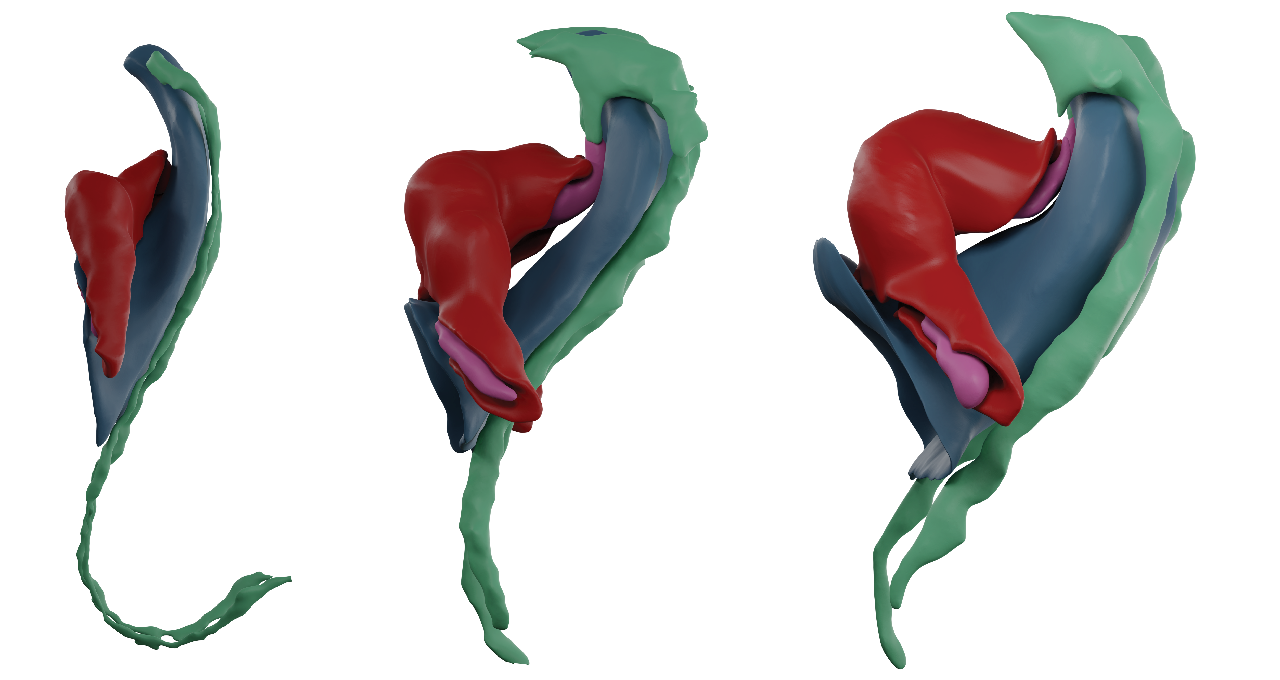
Publication in Nature Cardiovascular Research 2022
Pseudodynamic analysis of heart tube formation in the mouse reveals strong regional variability and early left–right asymmetry
In a collaboration with CNIC Madrid, we used surface mapping techniques to study the geometry of heart morphogenesis in mice. In the early mouse embryo, an initially flat piece of tissue develops into a heart tube within a time window of ~18 hours. Given a 3D dataset of multiple such tissues, we computed surface maps that allow both interpolation between different specimen and interpolation in time. The result is a time-continuous 3D reconstruction of the average growth process.
Isaac Esteban, Patrick Schmidt, Audrey Desgrange, Morena Raiola, Susana Temiño, Sigolène M. Meilhac, Leif Kobbelt, Miguel Torres. 2022. Nature Cardiovascular Research.
Course at Symposium on Geometry Processing 2021 Graduate School
Maps Between Surfaces
Together with Marcel Campen I gave a course on maps between surfaces at SGP 2021. We explained how to (1) computationally represent, (2) initially construct, and (3) numerically optimize maps. In particular, we focused on the class of surface homeomorphisms: maps that are continuous and bijective and thus can be used to faithfully transfer various kinds of surface data. We started with the well-studied case of maps in the plane and then worked our way up to the challenging case of maps between 3D surfaces.
Marcel Campen and Patrick Schmidt. 2021. Symposium on Geometry Processing Graduate School.
Publication at Symposium on Geometry Processing 2021
Surface Map Homology Inference
A continuous and bijective map between surfaces does not only determine a geometrical, but also a topological correspondence: It matches handles and tunnels and determines how paths twist around them. Many practical map representations (e.g. sampled maps) do not explicitly capture such aspects and can be topologically ambiguous in the presence of noise, outliers, or undersampling. We present a method to robustly infer topological information (a homology map) from an imperfect input map.
This paper received the Best Paper Award (1st Place) at SGP 2021 as well as the Graphics Replicability Stamp.
Janis Born, Patrick Schmidt, Marcel Campen, Leif Kobbelt. 2021. Computer Graphics Forum.
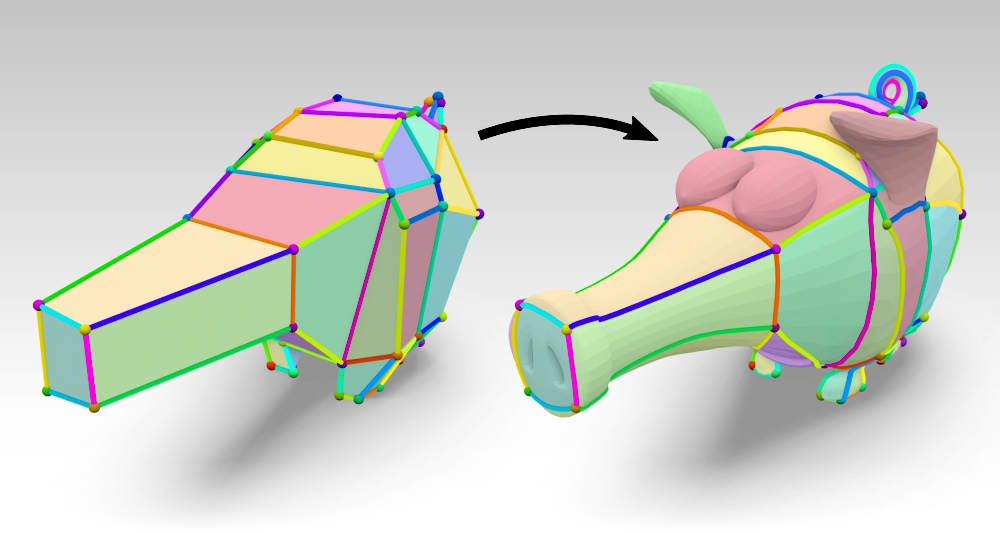
Publication at Eurographics 2021
Layout Embedding via Combinatorial Optimization
Embedding an abstract mesh connectivity into a surface is challenging, as avoiding intersections can easily cause excessively long paths. We compute an optimal order of shortest path insertions that minimizes total embedding length. The algorithm is used e.g. to prevent topological swirls in inter-surface map initialization.
This paper received an honorable mention for the Günter Enderle Best Paper Award at Eurographics 2021 as well as the Graphics Replicability Stamp.
Janis Born, Patrick Schmidt, Leif Kobbelt. 2021. Computer Graphics Forum.
Publication at SIGGRAPH 2020
Inter-Surface Maps via Constant-Curvature Metrics
We introduce a novel representation of maps between closed triangle meshes of the same genus. Our maps are guaranteed to be continuous, bijective and defined at every surface point. This map representation is via metrics of constant curvature, which—depending on the genus—induce either Euclidean, spherical or hyperbolic geometry. We are able to perform constructions in all three geometries in a unified way and optimize our maps for low surface-to-surface distortion.
Patrick Schmidt, Marcel Campen, Janis Born, Leif Kobbelt. 2020. ACM Transactions on Graphics.
Publication at SIGGRAPH Asia 2019
Distortion-Minimizing Injective Maps Between Surfaces
We compute injective maps between disk-topology surfaces by overlaying two parametrizations. Instead of optimizing both parametrizations individually, we show how to directly minimize distortion in the composed surface-to-surface map.
Patrick Schmidt, Janis Born, Marcel Campen, Leif Kobbelt. 2019. ACM Transactions on Graphics.
Publication at SIGGRAPH Asia 2016
Interactively Controlled Quad Remeshing of High Resolution 3D Models
We propose an interactive retopology workflow for generating high quality quad meshes from unstructured triangle meshes. The user is constantly provided with an automatically generated quad mesh, which can be modified by iteratively adding high-level constraints. To achieve updates at interactive speeds, we use a multiresolution approach and introduce both a novel decimation scheme and a coarse-to-fine mapping method.
Hans-Christian Ebke, Patrick Schmidt, Marcel Campen, Leif Kobbelt. 2016. ACM Transactions on Graphics.
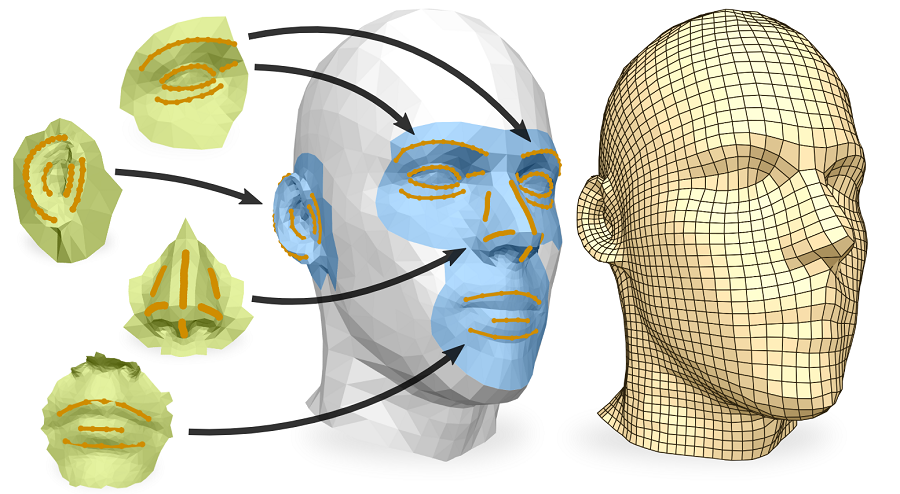
Master Thesis (2017)
Retrieval and Re-Embedding of Macro Constraints for Parametrization Based Quad Meshing
I developed a system that retrieves small surface patches from a database and embeds them on similarly curved regions of a target shape. Such patches carry user-defined information, e.g. feature curves, which can be used as constraints in interactive quad meshing scenarios. I designed an algorithm computing a smooth and injective map from each surface patch to a specified target region.
Bachelor Thesis (2014)
Towards Interactive Quadrangulation through Local Remeshing
I adapted the mixed-integer quadrangulation algorithm[1] to work within local surface regions. This modification allows for faster updates and more controlled user interactions. The local setting comes with new challenges in terms of singularity placement and constrained parametrization, that are not present in the original formulation.